Sparse Table (스파스 테이블) 특징
- 방향 그래프 입니다.
- 모든 점이 목적지가 있습니다.
- 그 점을 타고 새로운 점으로 갑니다.
- 2의 제곱근으로 도착한 점을 저장합니다.
(1번, 2번, 4번, 8번 이동에 대한 배열을 모두 저장합니다.)
예제를 풀면서 설명하겠습니다.
https://www.acmicpc.net/problem/17435
17435번: 합성함수와 쿼리
함수 f : {1, 2, ..., m}→{1, 2, ..., m}이 있다. 이때 fn : {1, 2, ..., m}→{1, 2, ..., m}을 다음과 같이 정의하자. f1(x) = f(x) fn+1(x) = f(fn(x)) 예를 들어 f4(1) = f(f(f(f(1))))이다. n과 x가 주어질 때 fn(x)를 계산하는
www.acmicpc.net
이 문제는 함수 f(x)가 있을 때 f3(x)는 < y= f(x) ----> z = f(y) ----> w = f(z) ----> result = w > 함수f(x)의 결과값을 다시 함수f(x)에 넣는걸 n번 반복하는 문제 입니다.
이 처럼 f(x)란 y라는 방향성을 가진 그래프로 표현이 가능합니다.
아래 그림은 1번쨰는 <2의 0승> 2번째는 <2의 1승> 3번째는 <2의 0승 후 2의 1승>을 한 결과 입니다.
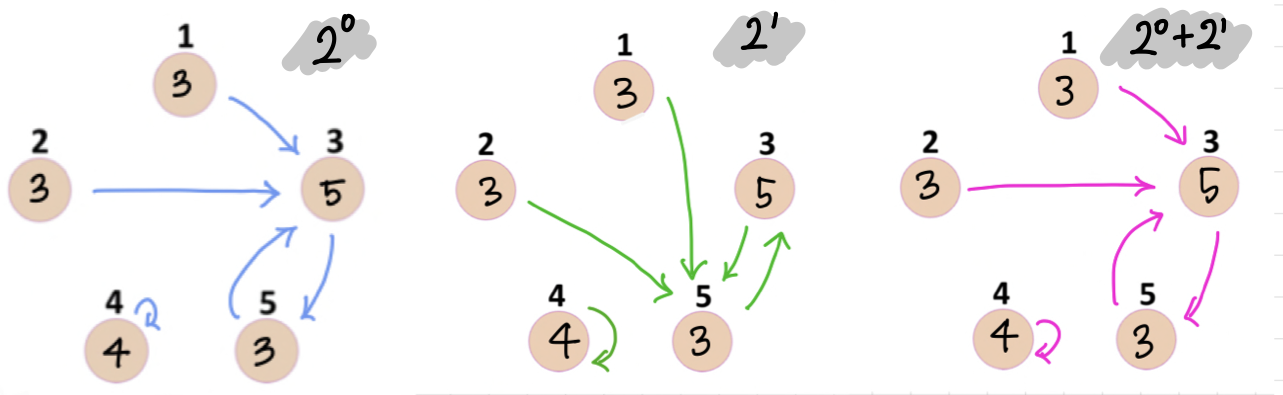
이를 테이블로 정리하면 아래와 같습니다.
| Table[x][y] | [1] | [2] | [3] | [4] | [5] |
| [0] | 3 | 3 | 5 | 4 | 3 |
| [1]= 2의 0승 | 5 | 5 | 3 | 4 | 5 |
| [2]= 2의 1승 | 3 | 3 | 5 | 4 | 3 |
| [3]= 2의 0승 + 2의 1승 | 5 | 5 | 3 | 4 | 5 |
Q. 왜 2의 제곱근일까?
2의 제곱근은 모든 수를 표현 할 수 있기 때문입니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 |
| 1000 | 1001 | 1002 | 1,003 | 1004 | |||||
| 0011 1110 1000 | 0011 1110 1001 | 0011 1110 1010 | 0011 1110 1011 | 0011 1110 1100 | |||||
문제에서 n이 1 ≤ n ≤ 500,000 사이의 수 이므로, 아래와 같은 범위를 가지게 됩니다.
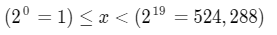
따라서 x는 0 ~ 18사이의 값이 될겁니다.
저희는 SparseTable[0][x]에 초기값을 넣었으므로 SparseTable[19][x] 까지 사용하면 되겠죠 ?

#include <iostream>
#include <vector>
using namespace std;
int SparseTable[20][200'001];
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int m;
cin >> m;
vector<int> vec;
for (int i = 1; i <= m; ++i)
{
int fm;
cin >> fm;
SparseTable[0][i] = (fm);
}
for (int i = 1; i < 20; ++i)
{
for (int j = 1; j <= m; ++j)
{
int temp = SparseTable[i - 1][j];
SparseTable[i][j] = SparseTable[i - 1][temp];
}
}
int q;
cin >> q;
while (q--)
{
int n, x;
cin >> n >> x;
int idx = x;
for (int k = 0; k < 20; k++)
{
if (n & (1 << k)) {
idx = SparseTable[k][idx];
}
}
cout << idx << "\n";
}
return 0;
}
끝.
ps. 요즘 짤툰 - 짐승친구들이 너무 재미있다. 김덕배 너무 귀여워 ~~!!!!

'👨🏻💻 programming > ◽ 알고리즘' 카테고리의 다른 글
| binary search & lower bound & upper bound [c++ 구현] (0) | 2024.07.05 |
|---|---|
| [Algorithm/ 비트마스크] (4) | 2023.02.17 |
| [Algorithm/Shortest Path] A* 알고리즘 - 구현C++ (0) | 2022.06.20 |
| [Algorithm/MST] 프림(Prim) 알고리즘 (0) | 2022.03.07 |
| [Algorithm/MST] 크루스칼(Kruscal) 알고리즘 (0) | 2022.03.03 |
