[Algorithm/Shortest Path] A* 알고리즘 - 구현C++

스터디에서 A* 알고리즘을 한 번 작성해보고 간단하게 콘솔로 띄어보고.. 유니티로 적용해보기로 하였다. 유니티로 옮기는 작업 벌써부터 걱정이 된다. 일단 A*알고리즘이 뭔지 정리를 해보자 ..

A* 알고리즘은 다익스트라 알고리즘을 확장하여 만들어진 알고리즘으로 주어진 출발 꼭짓점에서부터 목표 꼭짓점까지 가는 최단경로를 찾아내는 그래프 탐색 알고리즘 중 하나이다. 

주로 게임에서 몬스터가 플레이어를 목표지점으로 이동하거나  자동 사냥 게임에서 플레이어가 타겟(몬스터나 다른 PC)을 향해 이동시킬 때 사용하는 알고리즘이다. 

알고리즘	다익스트라 알고리즘	A* 알고리즘
목표점	시작점 -> 나머지 모든 정점들까지의 최단 거리	시작점 -> 목표점까지의 최단 거리
차후 경로 도출을 위한 함수 f(n)	현재 노드에서 가까운 노드부터 순차적으로 방문 f(n) = g(n)	현재 노드와 휴리스틱 함수를 통해 점수를 매기고 가장 좋은(가장 가까운) 점수 노드를 방문 f(n) = g(n) + h(n) (* h(n)=0 이면, 다익스트라)
속도	다익스트라 < A*

 

A* 알고리즘 방문 노드 탐색 기준 공식

$ f\big(n\big) = g\big(n\big)+h\big(n\big) $

- g(x): 시작 노드부터 현재 노드까지의 최단 거리(비용)

- h(x)/heuristic : 현재 노드에서 도착 노드까지의 추정된 남은 거리(비용)

 

heuristic 휴리스틱 중 대표적인 함수 

(1). 맨해튼 거리(Manhattan Distance) 함수 : L1 Distance라고 불리는 공식 

2차원 : |x1 - x2| + |y1 - y2|
3차원:  |x1 - x2| + |y1 - y2| + |z1 - z2| 

 

(2). 유클리디안 거리 함수(Euclidean Distance) : L2 Distance라고 불리는 공식 (아래 코드는 유클리디안 사용.)

2차원:  $$\sqrt{(x2-x1{)}^2+(y2-y1{)}^2}$$
3차원:  $$\sqrt{(x2-x1{)}^2+(y2-y1{)}^2+(z2-z1{)}^2}$$

---

그림으로 A*알고리즘 흐름보기

1. P = 시작점
2. P에 f, g, h 할당
3. Open 리스트에 P 넣기
4. B = Open 리스트에서 가장 낮은 f 값을 가진 노드
    a. B가 목표점이면, 경로 완성
    b. Open 리스트가 비었으면, 목표점까지 경로가 존재하지 않음
5. C = B에 연결된 노드
    a. C에 f, g, h 값 할당
    b. Open/Close 리스트에서 C가 있는지 체크
        1. 있으면, 더 낮은 f 값으로 경로 업데이트
        2. 없으면, C를 Open 리스트에 넣기
    c. 5번으로 돌아가서 B에 연결된 모든 노드를 대상으로 진행
6. 4번으로 돌아감

[pseudo 코드 출처]
A* 알고리즘의 구현 – 게임 개발 블로그/유니티/언리얼/스토리/팁/프로그래밍 (lunchballer.com)

[왼쪽]  각 노드간의 거리 (g(x)) ,  [오른쪽] 도착지점까지의 추정거리 (h(x))

시작노드 : 7번

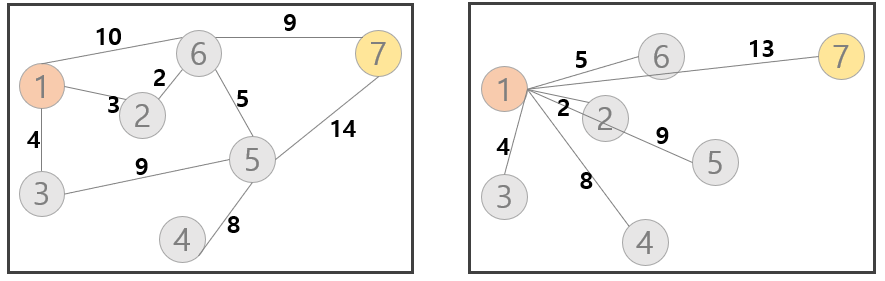
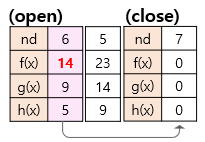
- 시작 노드 7번을 close에 담는다.
- 7번과 연결된 6번 5번을 open에 담는다.
- 추정거리가 가장 짧은 6번 노드를 close에 담는다.

 

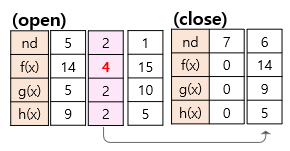
- 6번과 연결된 2번 1번을 open에 담는다.
- 추정거리가 가장 짧은 2번 노드를 close에 담는다.

 

 

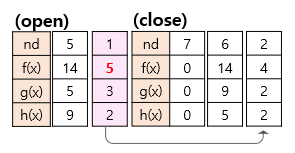
- 6번과 연결된 2번 1번을 open에 담는다.
- 추정거리가 가장 짧은 2번 노드를 close에 담는다.

 

 

---

구현 (C++)

	#include <iostream>
	#include <memory.h>
	#include <windows.h>
	#include <string>
	#include <queue>
	#include <algorithm>
	#include <math.h>
	using namespace std;
	#define MAX 31
	string gMap[MAX][MAX];
	bool visit[MAX][MAX];
	//대각선 포함 (순서: ↖ ↑ ↗ ← → ↙ ↓ ↘).
	int gStraight[4][2] = { { 0,-1 },{ -1, 0 },{ +1,0 },{ 0, +1 } };
	int gdiagonal[4][2] = { { -1,-1 },{ +1, -1 },{ -1, +1 },{ +1, +1 } };
	void DrawAStar(int pGrid);
	class AStar
	{
	public:
	POINT nPos;
	AStar* nParent;
	float gx;
	float hx;
	float fx;
	};
	struct compareAstar {
	bool operator()(AStar& lhs, AStar& rhs) {
	return lhs.fx > rhs.fx;
	};
	};
	int main(void)
	{
	cout << "======================================\n";
	cout << "========== AStar Algorithm ===========\n";
	cout << "======================================\n\n";
	cout << "격자 크기를 정해주세요(10~30)\n";
	int m_grid;
	cin >> m_grid;
	system("cls");
	if (m_grid >= 10 && m_grid <= 30) {
	for (int row = 0; row < m_grid; ++row) {
	for (int col = 0; col < m_grid; ++col) {
	gMap[row][col] = "□";
	cout << gMap[row][col];
	}
	cout << "\n";
	}
	}
	else
	{
	cout << "(10~30) 사이로 입력 하시라구요!\n";
	return 0;
	}
	cout << "시작 지점 (x, y)좌표와 도착지점 (x, y)좌표를 순서대로 적어주세요. \n";
	POINT m_start, m_goal;
	cin >> m_start.x >> m_start.y >> m_goal.x >> m_goal.y;
	m_start.x -= 1;
	m_start.y -= 1;
	m_goal.x -= 1;
	m_goal.y -= 1;
	gMap[m_start.y][m_start.x] = "★";
	gMap[m_goal.y][m_goal.x] = "★";
	DrawAStar(m_grid);
	memset(visit, false, sizeof(visit));
	cout << "A* 알고리즘을 실행시키려면 1을 입력해주세요.(종료는 0입력)\n";
	bool IsStart;
	cin >> IsStart;
	AStar CloseArray[MAX][MAX];
	const double INF = 1e9 + 7;
	for (int row = 0; row < m_grid; ++row) {
	for (int col = 0; col < m_grid; ++col) {
	CloseArray[row][col].fx = CloseArray[row][col].gx = CloseArray[row][col].hx = INF;
	CloseArray[row][col].nPos = { -1, -1 };
	CloseArray[row][col].nParent = nullptr;
	}
	}
	if (IsStart)
	{
	// 아직 조사하지 않은 상태를 담은 열린 목록
	// * decltype는 compare함수의 type을 정의하고 실제 compare함수는 constructor 패러미터로 전달해야한다는 뜻이다.
	//priority_queue< AStar, vector<AStar>, compareAstar> mOpenList;
	priority_queue< AStar, vector<AStar>, compareAstar> mOpenList;
	vector<AStar> mCloseList;
	AStar StartNode;
	StartNode.gx = 0;
	StartNode.hx = 0;
	StartNode.fx = 0;
	StartNode.nPos = { m_start.x , m_start.y };
	StartNode.nParent = nullptr;
	CloseArray[m_start.y][m_start.x].fx = CloseArray[m_start.y][m_start.x].gx = CloseArray[m_start.y][m_start.x].hx = 0.0f;
	visit[m_start.y][m_start.x] = true;
	mOpenList.push(StartNode);
	while (!mOpenList.empty())
	{
	AStar* nCurNode = new AStar(mOpenList.top());
	mOpenList.pop();
	visit[nCurNode->nPos.y][nCurNode->nPos.x] = true;
	if (gMap[nCurNode->nPos.y][nCurNode->nPos.x] != "★")
	gMap[nCurNode->nPos.y][nCurNode->nPos.x] = "☆";
	DrawAStar(m_grid);
	//Sleep(100);
	if (find_if(mCloseList.begin(), mCloseList.end(), [&](const AStar& parm)
	{return (parm.nPos.x == nCurNode->nPos.x) && (parm.nPos.y == nCurNode->nPos.y); }) != mCloseList.end())
	continue;
	mCloseList.push_back(*nCurNode);
	if (nCurNode->nPos.x == m_goal.x && nCurNode->nPos.y == m_goal.y)
	break;
	/*-------------------------------------------------------------------------------------*/
	for (int idx = 0; idx < 4; ++idx)
	{
	int nextPosX = nCurNode->nPos.x + gStraight[idx][0];
	int nextPosY = nCurNode->nPos.y + gStraight[idx][1];
	AStar nNextNode;
	if (nextPosX >= 0 && nextPosX <= m_grid && nextPosY >= 0 && nextPosY <= m_grid)
	{
	if (!visit[nextPosY][nextPosX]) {
	//휴리스틱 h(x)구하기 - 유클리디안(Euclidean) 거리 함수 사용
	float _hx = sqrt(pow(nextPosX - m_goal.x, 2) + pow(nextPosY - m_goal.y, 2));
	float _gx = nCurNode->gx + 1.0f;
	nNextNode.nPos = { nextPosX , nextPosY };
	nNextNode.fx = _hx + _gx;
	nNextNode.gx = nCurNode->gx + 1;
	nNextNode.hx = _hx;
	nNextNode.nParent = nCurNode;
	// mOpenList에 있는 노드라면 ???wj
	if (CloseArray[nextPosY][nextPosX].fx > nNextNode.fx ||
	CloseArray[nextPosY][nextPosX].fx == INF)
	{
	CloseArray[nextPosY][nextPosX].fx = _hx + _gx;
	CloseArray[nextPosY][nextPosX].gx = _gx;
	CloseArray[nextPosY][nextPosX].hx = _hx;
	CloseArray[nextPosY][nextPosX].nParent = nCurNode;
	mOpenList.push(nNextNode);
	}
	}
	}
	}
	/*-------------------------------------------------------------------------------------*/
	for (int idx = 0; idx < 4; ++idx)
	{
	int nextPosX = nCurNode->nPos.x + gdiagonal[idx][0];
	int nextPosY = nCurNode->nPos.y + gdiagonal[idx][1];
	AStar nNextNode;
	if (nextPosX >= 0 && nextPosX <= m_grid && nextPosY >= 0 && nextPosY <= m_grid)
	{
	if (!visit[nextPosY][nextPosX]) {
	//휴리스틱 h(x)구하기 - 유클리디안(Euclidean) 거리 함수 사용
	float _hx = sqrt(pow(m_goal.x - nextPosX, 2) + pow(m_goal.y - nextPosY, 2));
	float _gx = nCurNode->gx + 1.414f;
	nNextNode.nPos = { nextPosX , nextPosY };
	nNextNode.fx = _hx + _gx;
	nNextNode.gx = nCurNode->gx + 1;
	nNextNode.hx = _hx;
	nNextNode.nParent = nCurNode;
	// mOpenList에 있는 노드라면 ???
	if (CloseArray[nextPosY][nextPosX].fx > nNextNode.fx ||
	CloseArray[nextPosY][nextPosX].fx == INF)
	{
	CloseArray[nextPosY][nextPosX].fx = _hx + _gx;
	CloseArray[nextPosY][nextPosX].gx = _gx;
	CloseArray[nextPosY][nextPosX].hx = _hx;
	CloseArray[nextPosY][nextPosX].nParent = nCurNode;
	mOpenList.push(nNextNode);
	}
	}
	}
	}
	}
	gMap[mCloseList.back().nPos.y][mCloseList.back().nPos.x] = "♧";
	if (mCloseList.back().nParent != nullptr)
	{
	AStar* nNextNode = mCloseList.back().nParent;
	gMap[nNextNode->nPos.y][nNextNode->nPos.x] = "♧";
	while (nNextNode->nParent != nullptr)
	{
	gMap[nNextNode->nParent->nPos.y][nNextNode->nParent->nPos.x] = "♧";
	nNextNode = nNextNode->nParent;
	}
	}
	system("cls");
	for (int row = 0; row < m_grid; ++row) {
	for (int col = 0; col < m_grid; ++col) {
	cout << gMap[row][col];
	}
	cout << "\n";
	}
	}
	system("pause");
	return 0;
	}
	void DrawAStar(int pGrid)
	{
	system("cls");
	for (int row = 0; row < pGrid; ++row) {
	for (int col = 0; col < pGrid; ++col) {
	cout << gMap[row][col];
	}
	cout << "\n";
	}
	}

view raw gistfile1.txt hosted with ❤ by GitHub