[Algorithm/MST] 크루스칼(Kruscal) 알고리즘

크루스칼(Kruscal) 알고리즘 

최소 비용 신장트리(Minimum Spanning Tree) 대표적인 알고리즘 중 하나로 그래프 내의 모든 정점들을 가장 적은 비용으로 연결하기 위해 사용한 알고리즘이다. 

[Algorithm] 최소 비용 신장 트리 (MST, Minimum SpanningTree) (tistory.com)

[Algorithm] 최소 비용 신장 트리 (MST, Minimum SpanningTree)

이전에 포스팅한 최소 비용 신장 트리의 다섯까지 특징을 크루스칼 알고리즘에도 똑같이 적용된다.
1. 사이클이 없는 그래프
2. 가중치를 가진 그래프
3. 최소한의 연결을 한 그래프 ( N개의 정점 → N-1개의 간선 ) 
4. 트리 구조를 가지고 있는 그래프 
5. 대표적인 알고리즘은 프림, 크루스칼 알고리즘이 있다. 

크루스칼 알고리즘은 선택의 순간마다 눈앞에서 보이는 최적의 상황만을 쫒아 최종적인 해답에 도달하는 방법인 그리디 알고리즘의 일종이다. 즉, 그래프 간선들을 가중치의 오름차순으로 정렬하고 사이클을 형성하는 경우를 제외하고 정렬된 순서대로 간선을 선택한다. 이를 그림과 표로 알아보면 아래와 같이 표현할수 있다.

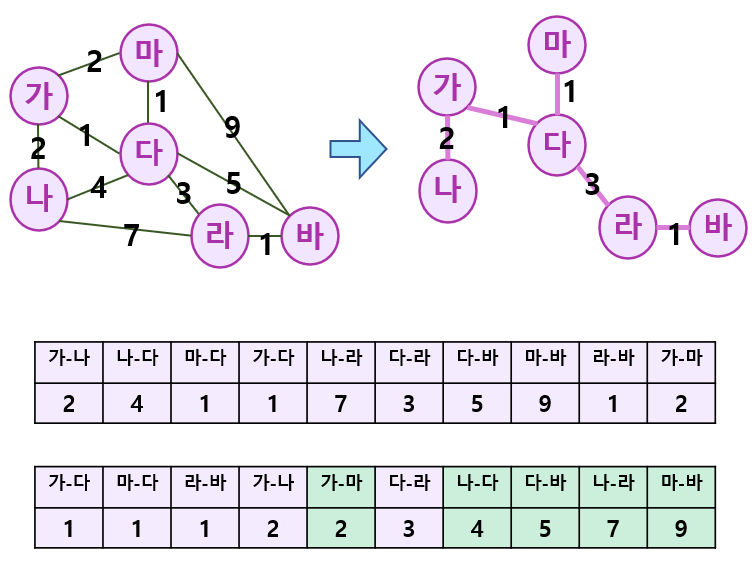
크루스칼 알고리즘은 간선의 개수가 E개 일 때, O(ElogE)의 시간 복잡도를 가진다.
크리스칼 알고리즘에서 시간이 가장 오래 걸리는 부분이 간선을 정렬하는 작업이며, E개의 데이터를 정렬했을 때의 시간 복잡도는 O(ElogE)이기 때문이고, 크루스칼 내부에서 사용되는 서로소 집합 알고리즘의 시간 복잡도는 정렬 알고리즘의 시간 복잡도보다 작으므로 무시한다.

 

	#include <iostream>
	#include <algorithm>
	#include <vector>
	using namespace std;
	using PIPII = pair<int, pair<int, int>>;
	int getParent(int* parent, int a)
	{
	if (parent[a] == a) return a;
	return parent[a] = getParent(parent, parent[a]);
	}
	void Union(int* parent, int a, int b)
	{
	a = getParent(parent, a);
	b = getParent(parent, b);
	if (a < b)
	parent[b] = a;
	else
	parent[a] = b;
	}
	int Find(int* parent, int a, int b)
	{
	a = getParent(parent, a);
	b = getParent(parent, b);
	if (a == b)
	return 1;
	else
	return 0;
	}
	int KrusKal(int* parent, vector<PIPII> edge, int vertex)
	{
	sort(edge.begin(), edge.end());
	int cnt = 0, idx = 0, ans = 0;
	while (cnt != vertex - 1)
	{
	int w = edge[idx].first;
	if (!Find(parent, edge[idx].second.first, edge[idx].second.second))
	{
	ans += w;
	Union(parent, edge[idx].second.first, edge[idx].second.second);
	idx++;
	cnt++;
	}
	else
	continue;
	}
	}

view raw gistfile1.txt hosted with ❤ by GitHub