728x90
반응형
" Algorithm/ KMP 알고리즘 "
🔸 KMP( Knuth, Morris, Prett ) Algorithm?
대표적인 상수시간 내에 할 수 있는 문자열 검색 알고리즘이다. 명칭은 알고리즘 쓰임새와 상관없이 만든 사람이름이다. 문자열 매칭 알고리즘이라고 부르는게(?) 더 좋을거 같다.
🔸 해답
https://www.acmicpc.net/problem/1786
"baekjoon 1786번 - 찾기"와 함께 kmp 알고리즘을 배우고 풀어보자.

- P: 패턴(길이: m) T: 텍스트(길이: n)
- 만약 모든 매칭을 하나하나 확인한다면? (n - m + 1) x m = 시간 복잡도 O(nm)
- 목표: 시간 목잡도 O(n) 만들기.
🔥 step 1. 찾으려는 문자열 전처리 과정 거치기
접두사(이을 접 : 接, 머리 두 : 頭)와 접미사(꼬리 미 : 尾) 최대 일치 길이를 구하기.
✔ 찾으려는 단어 : ABCDABD
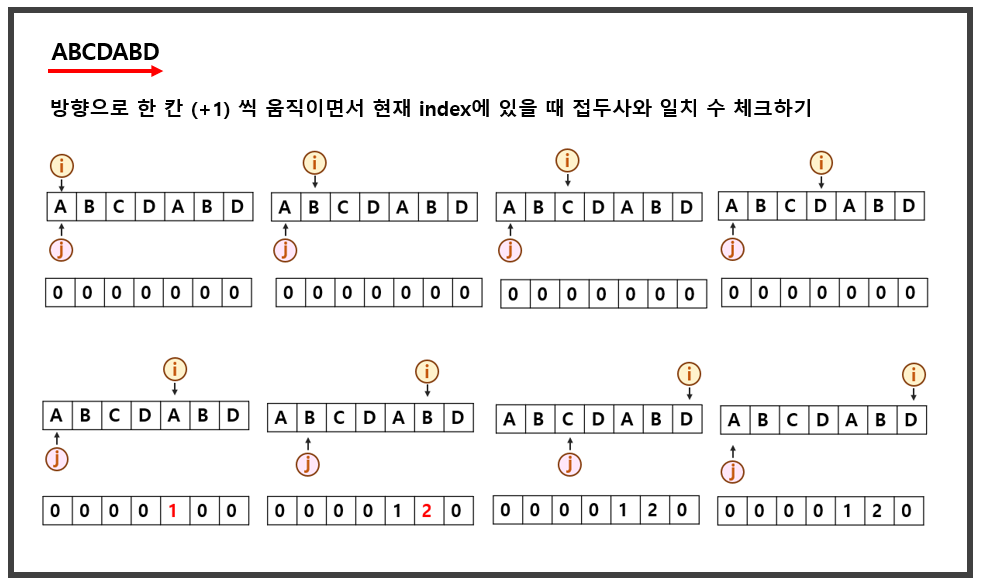
- 인덱스 [ i ]를 증가시키면서 인덱스[ j ]와 동일한 단어가 있는지 찾는다.
- 찾았다면 [ i ]와 [ j ] 둘다 증가 시킨다. j의 인덱스는 일치인 [ i ] 인덱스 번째 숫자 테이블에 ++j을 적는다.
- 만약 다른 부분이 발생했다면, j 는 숫자 테이블[ j - 1 ]의 수를 j에 입력한다.
void makeTable( string Pattern)
{
int j = 0;
for(int i = 1; i < Pattern.size(); ++i)
{
while( j > 0 && Pattern[i] != Pattern[j] )
{
j = numberTable[ j - 1 ];
}
if(Pattern[i] == Pattern[j])
{
nuberTable[i] = ++j;
}
}
}🔥 step 2. 만든 numberTable로 본문에서 문자열 찾기
나아가 만들어둔 숫자 테이블을 이용하여 main Text에서 찾고자 하는 단어를 찾아보자.
void KMP ( string mainText, string pattern )
{
int k = 0;
for(int i = 0 ; i < mainText.size(); ++i)
{
while( k > 0 && mainText[i] != pattern[k] )
{
k = numberTable[k - 1];
}
if( mainText[i] == pattern[k] )
{
if( k == mainText.size() - 1 )
{
k = numberTable[k];
}
else
{
k++;
}
}
}
}
728x90
반응형
'👨🏻💻 programming > ◽ 알고리즘' 카테고리의 다른 글
| [ Algorithm / 벨만 포드 알고리즘 ] + 백준 1865 웜홀 문제풀이 (2) | 2024.08.22 |
|---|---|
| binary search & lower bound & upper bound [c++ 구현] (0) | 2024.07.05 |
| [Algorithm/ 비트마스크] (4) | 2023.02.17 |
| [Algorithm/ Sparse Table (희소테이블)] 백준 17435번과 함께 (0) | 2023.02.01 |
| [Algorithm/Shortest Path] A* 알고리즘 - 구현C++ (0) | 2022.06.20 |
