3차원 공간에 대해서(좌표계, 변환, 카메라, 뷰)

1)  3차원 좌표계

3차원 공간의 세 기저 축 x,y,z에 대해 x → y → z → x → y 의 순서로 세 축이 순환된다고 생각해보자.

좌표계를 구분하는 방법은 x 에서 y로 가는 방향으로 손을 접었을때 엄지 손가락의 방향이다. 

 

2)  3차원 공간의 변환 

크기(Scale:S), 위치(Translation:T), 회전(Rotation:R) 

3차원 모델링 행렬곱의 순서는 Matrix = TRS

 

3) 카메라 공간

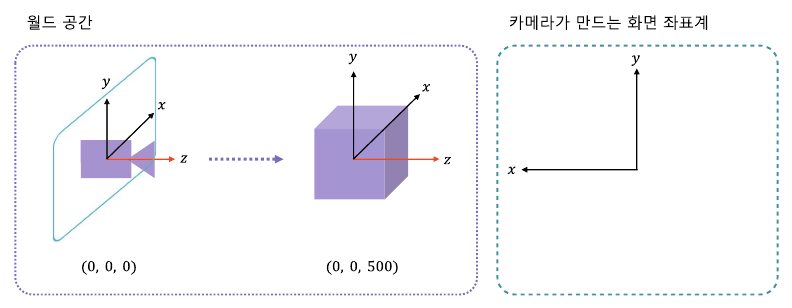
카메라에는 크기의 개념이 없기 때문에, 카메라의 트랜스폼은 크기 변환을 제외한 회전과 이동변환으로만 구성된다. 카메라의 트랜스폼에 저장된 위치 값을 T = (Tx, Ty, Tz)로 저장하고, 로컬 축 값을 각각 X = (Xx, Xy, Xz), Y = (Yx, Yy, Yz), Z = (Zx, Zy, Zz)로 지정해보면, 

※ 역행렬은 행렬 곱의 결과가 항등행렬이 나오는 특별한 행렬을 뜻한다. 

$$역행렬: A * A^{-1} =A^{-1} * A = I $$

결론: 크기 변환 S를 제외한 카메라의 트랜스폼으로부터 얻어지는 모델링 행렬 M은 

$$모델링 행렬: M = T*R,  뷰 행렬: M^{-1} = (T*R)^{-1} = R^{-1}* T^{-1}$$

 

※ 참고도서와 참고사이트를 확인하시려면 더보기를 눌려주세요

 http://www.yes24.com/Product/Goods/107025224

이득우의 게임 수학 - YES24