"(백준/ C++) 1010 - 다리 놓기 / 다이나믹 프로그래밍, 재귀"
https://www.acmicpc.net/problem/1010
N을 늘려보면서 비교를 해보니 규칙을 쉽게 발견 할 수 있었다.
N(강 서쪽)의 맨 위 다리가 M(강 동쪽)에 위치할 수 있는 조건은 N은 빠짐 없이 모두 연결은 되야 하므로 M - N + 1이 된다.
DP [ N ][ M ] 이라고 만들 때, 아래 그림과 같이 규직을 찾을 수 있는데 N이 1일때는 M의 개수 만큼 경우의 수가 생긴다. 이 조건은 함수의 return(반환) 조건으로 사용하면 된다.
또 N과 M이 같을 때는 모든 다리를 연결 하므로 언제나 하나의 경우의 수이다. 이거 또한 함수의 return(반환)조건으로 사용한다.
N(강 서쪽)의 맨 위 다리를 M(강 동쪽)에 있는 다리 위에서 부터 1이라고 했을 때 M - N + 1 번째 까지 아무대나 그어 보자. 그림을 보면 알지만 N(강 서쪽)의 맨 위 다리가 M에 어떤 위치에 있냐에 따라 경우의 수가 변화된다.

문제에 이러한 규칙이 있기 때문에 가능하다.
그럼 이렇게 해서 N(강 서쪽) : 3개의 사이트 M(강 동쪽) : 5개의 사이트가 있다고 가정할 때 다리끼리 서로 겹쳐지지 않고 다리를 지을 수 있는 경우의 수는 < DP [ 3 ][ 5 ] = DP [ 2 ][ 4 ] + DP [ 2 ][ 3 ] + DP [ 2 ][ 2 ] >이다.

// -----------------------------
// [ 다리 놓기 ] ----------------
// -----------------------------
#include<iostream>
using namespace std;
int dp[30][30] = {0, };
int BridgeFunc(int N, int M)
{
if (dp[N][M])
return dp[N][M];
if(N == M)
return dp[N][M] = 1;
if (N == 1)
return dp[N][M] = M;
for (int i = 1; i <= M-N+1 ; ++i)
{
dp[N][M] += BridgeFunc(N - 1, M - i);
}
return dp[N][M];
}
int main(void)
{
int mTC;
cin >> mTC;
while (mTC--)
{
int N, M; // 0 < N <= M < 30
cin >> N >> M;
cout << BridgeFunc(N, M) <<endl;
}
return 0;
}
+ 다른 분들 풀이를 보니 조합으로 풀고 있었다.
N(강 서쪽) : 3개의 사이트 M(강 동쪽) : 5개의 사이트가 있다고 가정할 때
이걸 5개 중 3개를 고르는 조합이라는 것이다 .. 그게 더 쉽네...허허
조합, 순열 공식만 한 번 더 보고 넘어가도록 하자
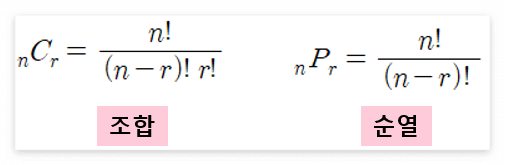

'📃 coding test > ◽ 백준' 카테고리의 다른 글
| (백준/c++) 14940 - 쉬운 최단 거리 / DFS, 그래프 (0) | 2024.08.16 |
|---|---|
| (백준/ C++) 12101- 1, 2, 3 더하기2 / 다이나믹 프로그래밍, 재귀 (0) | 2024.07.19 |
| (백준/ C++) 9095 - 1, 2, 3 더하기 / 다이나믹 프로그래밍, 재귀 (0) | 2024.07.19 |
| (백준/ C++) 1520 - 내리막길 / 다이나믹 프로그래밍 (1) | 2024.07.18 |
| (백준/ C++) 11049 - 행렬 곱셈 순서 / 다이나믹 프로그래밍 (1) | 2024.07.18 |
